Codeforces Round 1074 (Div. 4)

A. Perfect Root

分析

签到题

代码

void solve(){
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        cout<<i<<" \n"[i==n];
    }
}

B. Prefix Max

分析

还是签到题

代码

void solve(){
    int n;
    cin>>n;
    int mx=-1;
    for(int i=0;i<n;i++){
        int y;
        cin>>y;
        mx=max(y,mx);
    }
    cout<<(ll)mx*n<<endl;
}

C. Shifted MEX

分析

发现只要找一段最长的连续的序列就行了

代码

void solve(){
    int n;
    cin>>n;
    vector<int>vt(n+1);
    int mx=1;
    for(int i=1;i<=n;i++){
        cin>>vt[i];
    }
    sort(vt.begin()+1,vt.end());
    int ans=1;
    for(int i=2;i<=n;i++){
        if(vt[i]==vt[i-1]){
            continue;
        }
        if(vt[i]-vt[i-1]==1){
            ans++;
            mx=max(mx,ans);
        }
        else{
            ans=1;
        }
    }
    cout<<mx<<endl;

}

D. OutOfMemoryError

题意

懒得写了，自己读题吧

分析

如果一个数超过h，把数组重置一遍的话肯定会超时。所以我们可以拿个东西记录一下修改的数，我当时用了队列。

代码

void solve(){
    int n,m,h;
    cin>>n>>m>>h;
    vector<int>vt(n+1),flag(n+1,0);
    for(int i=1;i<=n;i++){
        cin>>vt[i];
    }
    queue<pair<int,int> >q;
    vector<int>vtt=vt;
    while(m--){
        int b,c;
        cin>>b>>c;
        vt[b]+=c;
        if(!flag[b]){
            flag[b]=1;
            q.push({b,vtt[b]});
        }
        if(vt[b]>h){
            while(!q.empty()){
                flag[q.front().first]=0;
                vt[q.front().first]=q.front().second;
                q.pop();
            }
        }
    }
    for(int i=1;i<=n;i++){
        cout<<vt[i]<<" \n"[i==n];
    }
}

E. The Robotic Rush

题意

有一条无限长的数轴，n个机器人在不同地方，还有m个尖刺和k个指令，如果碰到尖刺机器人就死亡，每输入一条指令后机器人还剩多少存活

分析

一个机器人肯定不会超越自己两边的尖刺，所以我们可以把机器人距离两边最近的尖刺的距离存下来，然后在每个指令之后判断机器人是否会死亡，总之就是一道麻烦一点的模拟题

代码

void solve(){
    int n, m, k;
    cin >> n >> m >> k;
    vector<int> bot(n + 1), pin(m + 1);
    for(int i = 1; i <= n; i++){
        cin >> bot[i];
    }
    for(int i = 1; i <= m; i++){
        cin >> pin[i];
    }
    string s;
    cin >> s;
    s = " " + s;
    
    sort(bot.begin() + 1, bot.end());
    sort(pin.begin() + 1, pin.end());
    vector<pair<int, int>> vtl, vtr;

    for(int i = 1; i <= n; i++){
        auto it = lower_bound(pin.begin() + 1, pin.end(), bot[i]);
        if(it == pin.end()){
        }
        else{
            vtr.push_back({*it - bot[i], i});
        }
        if(it != pin.begin() + 1){
            it--;
            vtl.push_back({bot[i] - *it, i});
        }
    }
    sort(vtl.begin(), vtl.end());
    sort(vtr.begin(), vtr.end());

    vector<bool> dead(n + 1, false);

    int step = 0; 
    int len = n;  
    int pl = 0, pr = 0;
    int mxl = 0, mxr = 0; 

    for(int i = 1; i <= k; i++){
        if(s[i] == 'L'){
            step--;
        }
        else{
            step++;
        }
        if(step > mxr){
            mxr = step;

            while(pr < vtr.size() && vtr[pr].first <= mxr){
                int id = vtr[pr].second;
                if(!dead[id]){
                    dead[id] = true;
                    len--;
                }
                pr++;
            }
        }
        else if(step < -mxl){
            mxl = -step;
            while(pl < vtl.size() && vtl[pl].first <= mxl){
                int id = vtl[pl].second;
                if(!dead[id]){
                    dead[id] = true;
                    len--;
                }
                pl++;
            }
        }
        cout << len << " ";
    }
    cout << endl;
}

F. BattleCows

题意

有$2^n$个堆，每个堆有一个权值为$a_i$的奶牛，并且一个堆的权值是一个桶里的奶牛的权值的异或和，然后进行若干轮比拼直到最后只剩一个堆，每次比拼，第$i(i为奇数)$的堆和第$i+1$的堆比拼，比拼后权值大的堆会压在权值小的堆上面，如果两个堆权值相同则左边的堆获胜。最后给你q次询问，每次询问两个数b和c，意思是把初始第b堆的牛的权值变为c，求最后有多少只牛在第b只牛头上

分析

可以用类线段树的思想，把对局看成一棵树，如下图

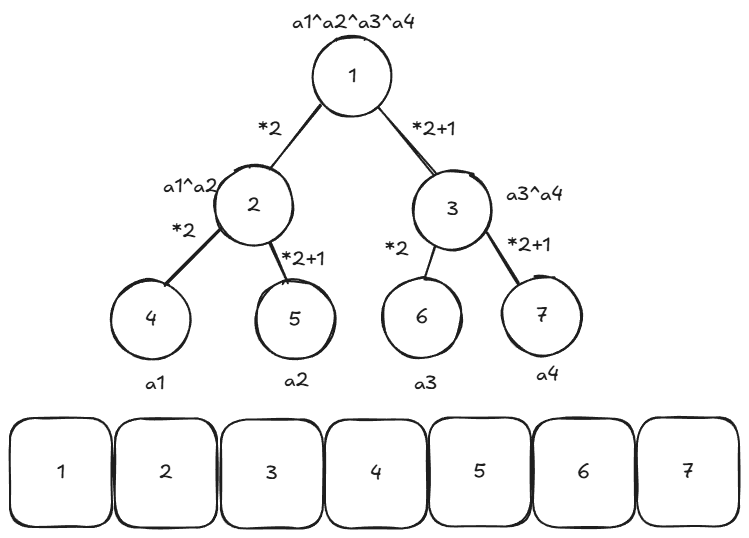
我们把奶牛的值作为叶子节点，根为叶子节点的异或和，从图中可以发现奶牛们的比赛持续n轮。

我们设$m=2^n$那么$a_i=tree_{m+i-1}$，并且 $tree_i=tree_{i \times 2} \oplus tree_{i \times 2+1}$ 这样就建好树了，当然也可以用建线段树的建法建数

对于每个询问，我们可以发现每一层只要修改一个数，所以复杂度是$O(\log n)$

对于每一局比赛，设当前的比赛轮数为$i$，如果要查询的这头牛输了，那么他头上会多出1<<(i-1)头牛

代码

#include <bits/stdc++.h>
#define ll long long
using namespace std;
int d[600005]; 
int a[600005]; 
int tree[600005];
int m;
void build(int u,int l,int r){
    if(l==r){
        tree[u]=a[l];
        return;
    }
    int mid=(l+r)/2;
    build(u*2,l,mid);
    build(u*2+1,mid+1,r);
    tree[u]=(tree[u*2]^tree[u*2+1]);
}
void upd(int t,int v){
    tree[t+m-1]=v;
    int u=t+m-1;
    while(u>1){
        u=u/2;
        tree[u]=tree[u*2]^tree[u*2+1];
    }
}
void solve() {
    int n, q;
    cin >> n >> q;
    m = 1 << n; 
    for(int i=1;i<=m;i++){
        cin>>a[i];
    }
    build(1,1,m);
    while(q--){
        int t,v;
        cin>>t>>v;
        int zq=a[t];
        upd(t,v);
        int u=t+m-1;
        int ans=0;
        for(int i=0;i<n;i++){
            if(u%2==0){
                if(tree[u]>=tree[u^1]){
                    ans+=0;
                }
                else{
                    ans+=(1<<i);
                }
            }
            else{
                if(tree[u]>tree[u^1]){
                    ans+=0;
                }
                else{
                    ans+=(1<<i);
                }
            }
            u=u/2;
        }
        upd(t,zq);
        cout<<ans<<endl;
    }
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    int t;
    cin >> t;
    while (t--) {
        solve();
    }
    return 0;
}